Galleria di stampe
|
DIVAGAZIONE SU GALLERIA
DI STAMPE DI M. C. ESCHER
|
|
DIVAGAZIONE SU GALLERIA
DI STAMPE DI M. C. ESCHER
|
|
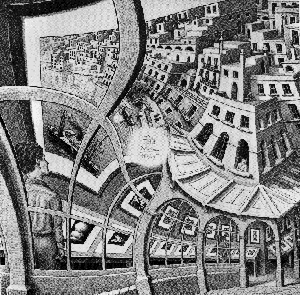
Più guardo, o meglio, più contemplo la litografia intitolata Galleria di stampe (1956) di Maurits Cornelis Escher, più, è il caso di dire, mi ci perdo. Vediamo, sulla sinistra, un giovane di spalle intento a guardare una stampa in cui è rappresentato il porto de La Valletta nell’isola di Malta, esposta in una galleria. |
| Fin qui non ci sarebbe niente di strano; la stranezza consiste nel fatto che la stampa si ingrandisce sotto gli occhi del giovane, e aumenta le sue dimensioni a tal punto da uscire dalla sua cornice fino a confondersi con il paesaggio esterno alla stampa e alla galleria; inoltre, se ci spostiamo con lo sguardo con moto circolare da sinistra verso destra, dall’alto verso il basso e seguendo la tettoia della galleria digradante verso il centro del quadro, ci ritroviamo all’ingresso della galleria medesima in cui il giovane di spalle è intento a guardare il paesaggio del porto de La Valletta, ritornando quindi esattamente là da dove eravamo partiti. Siamo qui in presenza di un paradosso “figurato” del genere Mani che disegnano (1948), in cui si vedono due mani ognuna della quali disegna l’altra, o anche del famoso triangolo impossibile del matematico Roger Penrose o degli altri oggetti impossibili di Escher, come le costruzioni fantastiche con il nastro di Moebius o il cubo tenuto in mano dal ragazzo seduto alla base della villa, anch’essa impossibile, nella litografia Belvedere (1958), raffigurabile sul piano ma non realizzabile nella spazio. Nella Galleria di stampe siamo continuamente rinviati dall’interno all’esterno e dall’esterno all’interno della galleria e della stampa osservata dal giovane, in una specie di moto perpetuo in cui i piani si mescolano e si intersecano tanto da non poter più capire dove finisca l’interno e dove cominci l’esterno, e viceversa. Nondimeno, così la stampa osservata dal giovane come il vapore e il gozzo nello specchio d’acqua del porto, La Valletta con i suoi tetti piatti, le sue torricelle, le sue cupolette e quelle rare e incantate presenze umane – un ragazzo seduto all’ombra su un terrazzo, una donna affacciata alla finestra che sembra guardare in direzione del giovane di spalle che osserva la stampa, due misteriose figurette di passanti vicino all’ingresso della galleria – stanno “dentro” la litografia che, data la sua autoreferenzialità e la compenetrazione di interno ed esterno, contiene se stessa; mentre noi che guardiamo il giovane che guarda la stampa, stiamo “fuori” di essa; ed è proprio standone fuori che possiamo vedere quell’incongruo “buco bianco” centrale, in cui l’artista ha pensato bene di mettere la sua firma: “MCE”. Incongruo?
|
 |
Possibile che l’artista non abbia voluto significare qualcosa con quel vuoto proprio al centro dell’opera? Non sarà che Escher, con quel “buco bianco” abbia voluto dirci che quella sua Galleria di stampe è rimasta in-compiuta, non finita e quindi in-finita? E’ questa l’interpretazione di Douglas R. Hofstadter: “Quel centro del vortice è, e deve essere, incompleto. Escher avrebbe potuto renderlo arbitrariamente piccolo ma non avrebbe potuto liberarsene. Quindi noi, dall’esterno, possiamo sapere che l’opera è essenzialmente incompleta, un fatto che il giovane, che è all’interno, non potrà mai sapere. |
|
Escher ha quindi dato una parabola figurativa del Teorema di Incompletezza di Goedel” (Goedel, Escher, Bach: un’Eterna Ghirlanda Brillante, Adelphi). Che cosa enuncia questo teorema? In parole semplici dice che tutte le assiomatizzazioni coerenti dell’aritmetica contengono proposizioni indecidibili, e anche che vi sono enunciati aritmetici veri ma indimostrabili, a meno che non divengano numeri essi stessi, in modo tale che si possano “interpretare gli enunciati dell’aritmetica a due diversi livelli: come enunciati dell’aritmetica e come enunciati su enunciati dell’aritmetica” (Ivi). Eppure forse c’era un modo per “completare” la Galleria di stampe: la soluzione (postuma) potrebbe offrirla la geometria frattale; questa affascinante geometria studia le figure che contengono figure esattamente o approssimativamente simili alla figura intera di cui fanno parte; fenomeno presente anche in natura: i rami di un abete sono simili all’abete, una felce ha le foglie composte di foglioline simili alla foglia-madre, un cavolfiore è composto di tanti piccoli cavolfiori… E non solo: in queste figure ogni parte è composta di parti più piccole che riproducono in scala l’intera figura, e così via. Anche la nostra litografia può essere letta come “una determinata curva ellittica sul piano dei numeri complessi che conduce a una sua ripetizione costante, ruotata in senso orario di circa 157 gradi e rimpicciolita di 22 volte. Insomma, in quel buco ci si potrebbe incastonare l’intera stampa rimpicciolita, dentro la quale ci si potrebbe mettere un’altra copia ancora rimpicciolita 22 volte, e così via all’infinito” (dal sito web “La Zattera”: I paradossi di Escher), innescando un vertiginoso moltiplicarsi dell’immagine iniziale, come quando si pongono due specchi uno di fronte all’altro, con un effetto di “fuga” che l’occhio può seguire ma fino a un certo limite, oltre il quale la può soltanto immaginare. Ecco, forse è proprio questo che mi rapisce nella Galleria di stampe: il trascorrere graduale da un paesaggio visibile a uno del tutto ideale, dalla concretezza di cose riconoscibili e familiari all’enigmaticità del loro messaggio, dalla rappresentazione di un oggetto impossibile esterno a quella di un oggetto impossibile interno, dalla figurazione realistica all’immaginazione onirica, dalla nitidezza e precisione dei contorni e dei particolari all’irrealtà prospettica e all’in-com-prensibilità dell’insieme, dal finito percepibile dai sensi all’infinitamente piccolo (e all’infinitamente grande) che è nascosto alla vista e nel cui vortice anche il pensiero, ben presto, s’annega… Fulvio Sguerso |